Quantifying the hierarchy of structural and mechanical length scales in granular systems
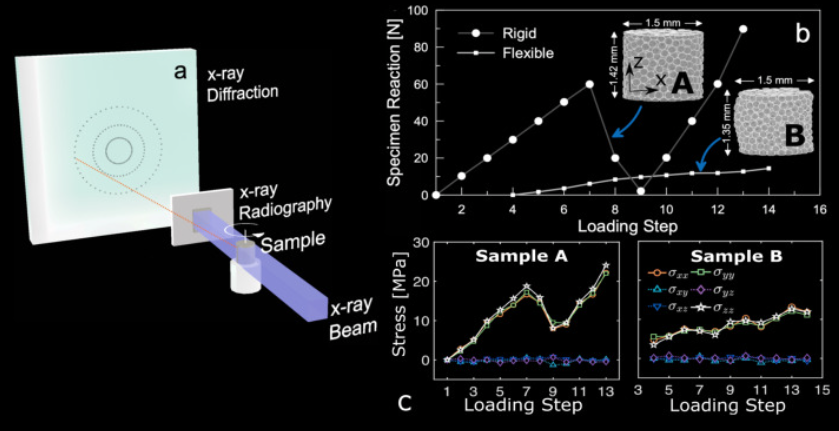
Continuum modeling of granular media is made possible by the existence of a length scale at and above which grain-resolved properties can be meaningfully homogenized. Progress has been made in identifying such length scales relevant to local structural properties such as porosity. However, a systematic analysis of scales above which different mechanical properties can be homogenized has yet to emerge. Here, X-ray tomography and 3D X-ray diffraction data are examined to identify such length scales. The data was obtained in-situ in compressed granular materials with rigid and flexible confinement. The experimental data are supplemented with validated discrete element simulations which examine different system sizes and different boundary conditions. Our study reveals a hierarchy in the length scales of granular solids, with lengths governing structural variables being the shortest, lengths of stress variables being intermediate, and lengths of energy dissipation being the longest. All structural and mechanical length scales obey a power law based on the theory of Geostatistics, implying that the length scales can be found by analyzing samples significantly smaller than the length scales themselves. The length scales are also found to be sensitive to boundary conditions, implying that they are extrinsic features of granular media.